그래프(Graph) 자료구조

5. 그래프 (Graph)

그래프(Graph)는 정점(Vertex)과 정점 간의 관계를 나타내는 간선(Edge)으로 구성된 자료구조입니다. 그래프는 트리와는 달리 순환을 허용하며, 비선형 구조로 다양한 관계를 모델링할 수 있습니다. 그래프는 소셜 네트워크 분석, 네트워크 경로 탐색, 지도에서의 최단 경로 등 다양한 문제를 해결하는 데 활용됩니다.

5.1 그래프의 기본 개념

그래프는 다음과 같은 주요 구성 요소로 이루어져 있습니다:

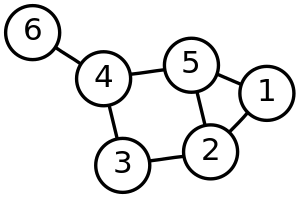
정점(Vertex): 데이터를 저장하는 그래프의 노드입니다.
간선(Edge): 두 정점을 연결하는 선으로, 정점 간의 관계를 나타냅니다.
차수(Degree): 하나의 정점에 연결된 간선의 개수를 나타냅니다.
경로(Path): 한 정점에서 다른 정점으로 가는 경로를 의미합니다.

5.2 그래프의 종류

그래프는 연결 방식에 따라 여러 종류로 나뉩니다:

무방향 그래프(Undirected Graph): 간선이 방향을 가지지 않는 그래프입니다. 두 정점 간의 연결은 쌍방향입니다.
유방향 그래프(Directed Graph): 간선이 방향을 가지는 그래프입니다. 한쪽 방향으로만 연결될 수 있습니다.
가중치 그래프(Weighted Graph): 간선에 가중치가 부여된 그래프입니다. 예를 들어, 두 정점 간의 거리나 비용을 나타낼 때 사용됩니다.
사이클이 있는 그래프(Cyclic Graph): 정점에서 출발하여 다시 자신에게 돌아올 수 있는 경로가 존재하는 그래프입니다.
사이클이 없는 그래프(Acyclic Graph): 정점에서 자신으로 돌아오는 경로가 없는 그래프입니다.

5.3 그래프 표현 방법

그래프는 주로 두 가지 방식으로 표현됩니다:

인접 행렬(Adjacency Matrix): 그래프를 2차원 배열로 표현하는 방법으로, 정점 간의 연결 여부를 행렬로 나타냅니다. 행렬의 값이 1이면 두 정점이 연결되어 있다는 의미입니다.
인접 리스트(Adjacency List): 각 정점에 대해 연결된 정점들의 리스트로 그래프를 표현합니다. 인접 리스트는 메모리 효율이 좋습니다.

예제: 인접 리스트를 사용한 그래프 구현

# 인접 리스트를 이용한 그래프 구현
class Graph:
    def __init__(self):
        self.graph = {}  # 그래프를 딕셔너리로 표현

    # 정점을 추가하는 함수
    def add_vertex(self, vertex):
        if vertex not in self.graph:
            self.graph[vertex] = []

    # 간선을 추가하는 함수 (양방향 간선)
    def add_edge(self, vertex1, vertex2):
        if vertex1 in self.graph and vertex2 in self.graph:
            self.graph[vertex1].append(vertex2)
            self.graph[vertex2].append(vertex1)

    # 그래프 출력 함수
    def print_graph(self):
        for vertex in self.graph:
            print(f"{vertex} -> {self.graph[vertex]}")

# 그래프 생성
g = Graph()

# 정점 추가
g.add_vertex(1)
g.add_vertex(2)
g.add_vertex(3)
g.add_vertex(4)

# 간선 추가
g.add_edge(1, 2)
g.add_edge(1, 3)
g.add_edge(2, 4)

# 그래프 출력
g.print_graph()  # 출력: 1 -> [2, 3], 2 -> [1, 4], 3 -> [1], 4 -> [2]

5.4 그래프 탐색 알고리즘

그래프에서 특정 데이터를 찾거나 경로를 찾기 위해 탐색 알고리즘을 사용합니다. 대표적인 탐색 알고리즘에는 다음 두 가지가 있습니다:

너비 우선 탐색(BFS, Breadth-First Search)

BFS는 그래프를 넓게 탐색하는 방식입니다. 시작 정점에서 가까운 정점부터 탐색하며, 큐(Queue)를 사용해 탐색이 진행됩니다.

from collections import deque

def bfs(graph, start):
    visited = set()  # 방문한 정점을 저장할 집합
    queue = deque([start])  # 큐에 시작 정점을 추가

    while queue:
        vertex = queue.popleft()  # 큐에서 정점을 꺼냄
        if vertex not in visited:
            print(vertex, end=" ")
            visited.add(vertex)  # 정점을 방문 처리
            queue.extend(graph[vertex])  # 인접한 정점을 큐에 추가

# 그래프 정의 (인접 리스트)
graph = {
    1: [2, 3],
    2: [4],
    3: [],
    4: []
}

# BFS 실행
bfs(graph, 1)  # 출력: 1 2 3 4

깊이 우선 탐색(DFS, Depth-First Search)

DFS는 그래프를 깊게 탐색하는 방식으로, 스택(Stack) 또는 재귀(Recursion)를 사용합니다. 한 정점에서 갈 수 있는 깊은 곳까지 탐색한 후 돌아와서 다른 경로를 탐색합니다.

def dfs(graph, start, visited=None):
    if visited is None:
        visited = set()  # 방문한 정점을 저장할 집합
    visited.add(start)
    print(start, end=" ")

    # 인접한 정점을 재귀적으로 방문
    for neighbor in graph[start]:
        if neighbor not in visited:
            dfs(graph, neighbor, visited)

# DFS 실행
dfs(graph, 1)  # 출력: 1 2 4 3

5.5 그래프의 응용

그래프는 다양한 분야에서 응용될 수 있습니다. 대표적인 응용 사례는 다음과 같습니다:

소셜 네트워크 분석: 사람들 간의 관계를 그래프로 나타내고, 친구 추천 알고리즘에 활용됩니다.
지도에서의 최단 경로 탐색: 도시 간의 도로망을 그래프로 나타내어, 최단 경로를 찾는 문제에 사용됩니다.
컴퓨터 네트워크: 라우팅 문제에서 그래프를 사용하여 데이터 전송 경로를 최적화합니다.

설화스터디 소프트웨어학과

[자료구조개론] 5. 그래프 완벽 설명