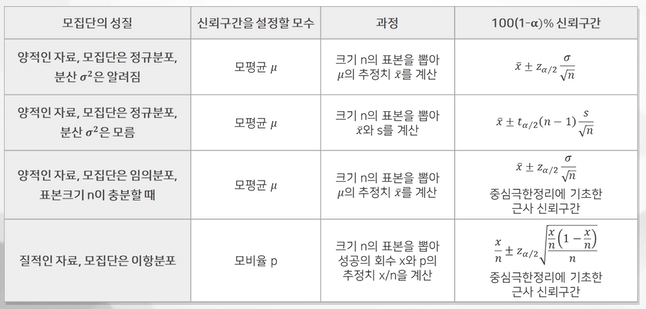
1) 모평균
-모집단이 정규분포, 분산이 알려진 경우
-모집단이 정규분포, 분산을 모르는 경우
-모집단이 임의분포, 표본크기가 n으로 충분히 큰 경우
$$ x=\frac{-b+\sqrt{b^{2}-4ac}}{2a} $$
2) 모비율
-Z1, ...Zn은베르누이 분포에서 확률표본


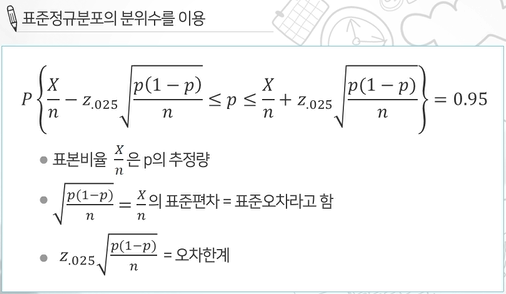

3) 표본 크기 결정
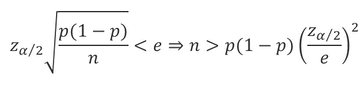
-이전 연구에서 사용한 p*가 존재하는 경우
-소표본으로 p를 추정한 추정치 p^을 이용하여 n을 계산한 후 필요한 표본을 더 추출하는 경우
-표준오차의 최대값을 사용
4) 모평균 및 모비율의 신뢰구간 구하기
출처: https://thegap.tistory.com/170 [theGAP (SecureDog):티스토리]
지지율, 시청률, 실업률 따위와 같이 모집단에서 어떤 사건에 대한 비율을 모비율이라 하고 기호로 pp로 쓴다. 또 그 모집단에서 임의추출한 표본에서 그 사건의 비율을 표본비율이라 하고 기호로 ^pp^로 쓴다. 일반적으로 어떤 사건에 대한 표본비율은 다음과 같이 구한다.
크기가 n인 표본에서 어떤 사건이 일어난 횟수를 확률변수 X라고 할 때, 그 사건에 대한 표본비율 p^은
p^=Xn
표본비율 ^p=Xnp^=Xn에서 확률변수 XX는 확률이 pp인 nn번의 독립시행에서 그 사건이 일어난 횟수이므로 이항분포 B(n,p)B(n,p)를 따른다. 이항분포 B(n,p)B(n,p)를 따르는 확률변수 XX의 평균과 분산이
E(X)=np,V(X)=npqE(X)=np,V(X)=npq (단, q=1−pq=1−p)
이므로 표본비율 ^pp^의 평균과 분산, 표준편차는 다음과 같다.
E(^p)=E(Xn)=1nE(X)=pE(p^)=E(Xn)=1nE(X)=p
V(^p)=V(Xn)=1n2V(X)=pqnV(p^)=V(Xn)=1n2V(X)=pqn
σ(^p)=√V(^p)=√pqnσ(p^)=V(p^)=pqn
일반적으로 표본크기 nn이 충분히 클 때, 표본비율은 정규분포 N(p,pqn)N(p,pqn)를 따른다고 알려져 있다.
(참고 np≥5,n(1−p)≥5np≥5,n(1−p)≥5이면 nn이 충분히 크다고 생각한다.)
표본비율 p^의 분포
표본비율 p^의 분포는 표본크기 n이 충분히 클 때, 정규분포 N(p,pqn)를 따른다.
이를 표준화한 Z=p^−ppqn는 표준정규분포 N(0,1)을 따른다. (단, q=1−p)
이를 바탕으로 모비율을 추정한다.
표본크기 nn이 충분히 클 때, 표본비율 ^pp^의 분산 pqnpqn에서 p,qp,q값 대신 표본비율 ^p,^qp^,q^을 사용한 Z=^p−p√^p^qnZ=p^−pp^q^n도 표준정규분포 N(0,1)N(0,1)을 따른다는 것이 알려져 있다.
표준정규분포에서 P(−1.96≤Z≤1.96)=0.95P(−1.96≤Z≤1.96)=0.95이므로
P(−1.96≤^p−p√^p^qn≤1.96)=0.95P(−1.96≤p^−pp^q^n≤1.96)=0.95
P(^p−1.96√^p^qn≤p≤^p+1.96√^p^qn)=0.95P(p^−1.96p^q^n≤p≤p^+1.96p^q^n)=0.95
[^p−1.96√^p^qn,^p+1.96√^p^qn][p^−1.96p^q^n,p^+1.96p^q^n]를 신뢰도 95% 신뢰구간이라고 한다.
신뢰도 99% 신뢰구간은 [^p−2.58√^p^qn,^p+2.58√^p^qn][p^−2.58p^q^n,p^+2.58p^q^n]이다
출처: https://suhak.tistory.com/131 [수학과 사는 이야기:티스토리]
'통계 > 기초통계' 카테고리의 다른 글
| [통계] [기초통계] 왜도 skewness 설명 (0) | 2024.01.19 |
|---|---|
| [통계] [기초통계] 공분산과 상관관계 (0) | 2024.01.19 |
| [통계] [기초통계] 베르누이분포 설명 (0) | 2024.01.19 |
| [통계] [기초통계] 3. 조건부 확률 설명 (1) | 2024.01.19 |
| [통계] [기초통계] 2. 정규분포 설명 (1) | 2024.01.19 |



