Covariance(공분산)
공분산은 두 변수가 변화할 때 어떤 연관성이 있는지를 나타내는 척도이다.
=> 한 변수가 변했을 때 다른 변수의 변화량에 얼마나 영향을 주는가?
(ex: BMI지수와 성인병의 발병률은 어떤 연관성이 있는가?)
분산V= Sigma( (X-E)^2 ) / N= E((X- E(X))^2)
공분산Cov= E( (X-E(X) * (Y-E(Y)) )
공분산은 각 변수가 각 평균에서 떨어진 만큼의 거리의 평균을 의미한다.
공분산 값(양수/음수)에 따라 어떤 연관성이 있는지를 알아낼 수 있다.

위와 같이 cov가 양수이면 X가 증가할 때 Y도 증가하고,
cov가 음수이면 X가 증가할 때 Y는 감소하는 양상을 띈다.
그러나 cov의 절대값이 큰 것이 연관관계가 크다는 것을 의미하지는 않는다는 것에 주의하자.
(분산이 큰 변수끼리는 연관성에 관계없이 공분산도 크게 나올 수 있다)
Correlation(상관관계)
공분산이 "연관성이 존재하는가?"에 초점을 맞추었다면
상관관계는 "그럼 얼마나 연관성이 있는가?"에 초점을 맞춘다.
Cov(xy)= E( (X-E(X)) * (Y- E(Y)) )
Correlation(xy)= r= Cov(xy)/(S(x)*S(y))
S(x)는 x의 표준편차(Standard deviation)
S(y)는 y의 표준편차
상관관계는 강도(r)로 나타나고, 공분산을 각 변수의 표준편차의 곱으로 나눈 값으로 구할 수 있다.
강도(r)은 [-1, 1] 사이값으로 나타난다.
그 이유는 아래와 같다.
//자기자신간의 공분산은 정의에 의거해 표준편차의 제곱과 같다
Cov(xx)= S(x)* S(x)
//따라서 아래가 성립한다
Cov(xx)/(S(x)*S(x))= 1
Cov(xy)<= S(x)* S(y) // 공분산과 표준편차 정의에 따라서
-1<=Cov(xy)/(S(x)* S(y))<= 1 //공분산은 음수일 수도 있으므로
다시 상관관계를 구하는 식으로 돌아가서, Z 스코어 표준화를 진행하면 아래와 같다.
Z표준화 시, Z= (X- M)/S= (변수- 평균)/표준편차
이므로
r= Cov(x,y)/(S(x)*S(y))= Sigma(z(x)*z(y))/ N
로도 표현할 수 있다
r= Sigma(z(x)* z(y))/N 으로 나타낸 것을 Pearson correlation coefficient(피어슨 상관 계수)라고 한다.

이 상관 계수를 통해 데이터의 변화 형태를 유추할 수 있다.
Covariable과는 달리 Correlation을 통해 얼마나 연관 강도가 있는지를 알아낼 수 있기 때문이다.
(if r<0, x가 증가할 때 y는 감소)
(if r>0, x가 증가할 때 y도 증가)
Covariance(공분산) vs Correlation(상관관계)
Covariance: 두 변수의 선형 관계의 방향을 알려준다.
Covariance: 두 변수의 선형 관계의 방향과 강도까지 알려준다.
출처: https://satisfactoryplace.tistory.com/302 [만족:티스토리]

4.3 서로 독립인 두 개의 랜덤 변수 Bivariate Independent Random Variables 페이지에서 두 랜덤 변수가 독립인 경우를 다루었다. 하지만 현실에서 측정치나 통계치들은 서로 연관되어 있는 경우가 훨씬 많다. 예를 들어, 한라산에서 각 지점의 고도와 온도를 측정하는 경우, 고도가 높을 수록 온도가 낮게 측정될 것이다. 또 다른 예로 종이의 크기와 무게를 측정하는 경우에도 이 두 값은 서로 연관되어 있다. 이 페이지에서는 이렇게 서로 연관되어 있는 랜덤 변수들이 얼마나 하게 연결되어 있는지를 보여주는 여러 지표 중 공분산과 상관계수에 대하여 살펴볼 것이다.
#Relation Between Random Variables?
먼저 랜덤 변수들이 강한 연관 관계에 있다는 것이 어떤 의미인지에 대하여 생각해보자. 앞에서 예로 든 종이의 크기와 무게는 거의 완벽히 연결되어 있다. 종이가 크면 무게도 무겁고, 종이가 작으면 무게도 가볍다. 종이에 대한 충분한 데이터가 주어진다면 종이의 크기만 알아도 무게를 계산해 낼 수 있고, 반대로 종이의 무게만 알아도 크기를 계산해 낼 수 있을 것이다. 그러나 성인의 키와 몸무게는 서로 연관되어 있지만 강하게 연결되어 있다고 할 수 없다. 보통은 키가 크면 몸무게가 더 나가겠지만, 꼭 키가 큰 사람이 작은 사람보다 몸무게가 더 나가는건 아니다. 따라서 키를 알아낸다고 해서 몸무게를 정확히 계산할 수 없고, 반대로 몸무게를 알아낸다고 해서 키를 정확히 계산해 낼 수는 없다. 즉, 강한 연관 관계인 경우에는 랜덤 변수들이 정확히 함수 관계에 있다고 할 수 있지만, 약한 약한 연관 관계인 경우에는 랜덤 변수들이 대략적으로만 특정 경향성을 가진다고 할 수 있다.
이번 페이지에서는 수식의 가독성을 위하여, � 의 평균을 �[�] 대신 ��, 분산을 Var(�) 대신 ��2 으로 표기한다.
#Covariance, Correlation
DEFINITION
Random variable � 와 � 에 대하여, 다음 값을 � 와 � 의 covariance(공분산)이라고 부른다.
Cov(�,�)=�[(�−��)(�−��)]
DEFINITION
Random variable � 와 � 에 대하여, 다음 값을 � 와 � 의 correlation 또는 correlation coefficient(상관 계수)라고 부른다.
���=Cov(�,�)����
당연히 실제 계산은 joint distribution에서 이루어진다. 예를 들어 � 와 �가 연속인 경우, covariance는 다음과 같이 joint pdf의 적분을 통해 계산할 수 있다.
Cov(�,�)=∫(�−��)(�−��)��,�(�,�) ����
보통 covariance를 계산하기 위해 위의 정의를 그대로 사용하기 보다는 다음과 같은 형태로 변형하여 계산한다.
THEOREM
Cov(�,�)=�[��]−����
(증명)
Cov(�,�)=�[(�−��)(�−��)]=�[��−���−���+����]=�[��]−���[�]−���[�]+����=�[��]−����−����+����=�[��]−����
(증명 끝)
#Basic Properties of Covariance
Covariance는 다음과 같은 특징들을 갖는다.
THEOREM
Random variable �, �, �, �, 상수 �, �, �, � 에 대하여 다음이 성립한다.
1. Cov(�,�)=Var(�)
2. Cov(�,�)=0
3. Cov(�,�)=Cov(�,�)
4. Cov(��,��)=��Cov(�,�)
5. Cov(�+�,�+�)=Cov(�,�)
6. Cov(��+��,��+��)=��Cov(�,�)+��Cov(�,�)+��Cov(�,�)+��Cov(�,�)
(증명)
1. variance의 정의와 covariance의 정의로부터 바로 얻어진다.
2. 상수 � 를 random variable처럼 이해하면, � 의 평균은 � 가 되므로 covariance의 정의로부터
Cov(�,�)=�[(�−��)(�−�)]=0
3. covariance의 정의로부터
Cov(�,�)=�[(�−��)(�−��)]=�[(�−��)(�−��)]=Cov(�,�)
4. random variable �� 와 �� 의 평균은 각각 ���, ���가 되므로
Cov(��,��)=�[(��−���)(��−���)]=�[��(�−��)(�−��)]=���[(�−��)(�−��)]=��Cov(�,�)
6. random variable ��+�� 와 ��+�� 의 평균은 각각 ���+���, ���+��� 이므로
Cov(��+��,��+��)=�[(��+��−���−���)(��+��−���−���)]=�[{�(�−��)+�(�−��)}{�(�−��)+�(�−��)}]=�[��(�−��)(�−��)]+�[��(�−��)(�−��)] +�[��(�−��)(�−��)]+�[��(�−��)(�−��)]=��Cov(�,�)+��Cov(�,�) +��Cov(�,�)+��Cov(�,�)
(증명 끝)
#Covariance and Correlation of Indepedent Random Variables
왜 covariance와 correlation이 random variable들 사이의 연관 관계를 나타내는 값이라고 할까? 다음 정리를 살펴보자.
THEOREM
Random variable � 와 � 가 서로 독립이면, Cov(�,�)=0 이다.
(증명)
� 와 � 가 서로 독립이면, �[��]=�[�]�[�]=���� 이므로, 식 (???)로부터 Cov(�,�)=0.
(증명 끝)
따라서 독립인 경우 correlation도 0이 된다. 위 정리로부터 covariance나 correlation이 0이 아닌 값을 가지는 경우, 두 random variable은 서로 독립이 아니라는 뜻이 된다.
Example 1
다음과 같은 joint pdf에 대하여 covariance와 correlation을 구해보자.
��,�(�,�)=1 , 0<�<1 and �<�<�+1
먼저 ��, ��2, ��, ��2 를 구하기 위해, 각 random variable의 marginal pdf를 구하면,
��(�)=∫��+1��,�(�,�) ��=1
��(�)={∫0���,�(�,�)��=�when 0<�<1∫�2��,�(�,�)��=2−�when 1≤�<2
따라서,
��=12��2=112��=1��2=16
이제 covariance를 계산하기 위하여 �[��] 를 계산하자.
�[��]=∫01∫��+1�� ����=712
식 (???)를 이용하여,
Cov(�,�)=�[��]−����=112
그리고 correlation의 정의를 이용하여,
���=Cov(�,�)����=1����2
비교를 위하여 또 다른 joint pdf에 대하여 똑같은 계산을 해보자.
��,�(�,�)=10 , 0<�<1 and�<�<�+110
같은 방식으로 covariance와 correlation을 구해보면
Cov(�,�)=112���=100101
이 두 joint pdf의 support를 좌표평면에서 살펴보면 다음과 같다.
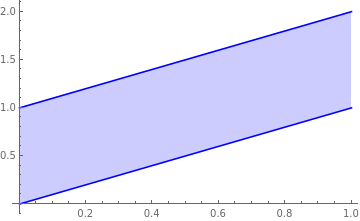

��,� 와 ��,� 의 분포를 비교해보면, ��,� 의 경우 � 가 더 넓게 균등히 분포해 있기 때문에 이 페이지 처음 논의에 의하면, 더 약한 연관 관계에 있다고 할 수 있다. ��,� 의 경우 � 값을 알게 되면, � 는 상당한 정확도로 값을 예측할 수 있기 때문에 더 강한 연관 관계라고 할 수 있을 것이다. 그러나 covariance 값은 두 경우 모두 112 로 동일하다. 이는 각 경우 variance가 서로 다르기 때문인데, 이렇게 두 연관 관계를 서로 비교하는 경우에는 covariance의 값을 standard deviation으로 나눈 correlation이 더 유용한 값이라는 것을 알 수 있다.
#Linear Relation
covariance와 correlation에서 주의해야 할 것은, 위 정리의 역은 성립하지 않는다는 것이다. 즉, 두 random variable이 독립이면 covariance와 correlation이 0이지만, 반대로 covariance와 correlation이 0이라고 해서 두 random variable이 반드시 독립인건 아니다. 다음의 예제를 살펴보자.
Example 2
Random variable � 는 uniform (−1,1) distribution을 따르고 � 와 독립인 random variable � 는 uniform (0,110) distrubution을 따른다고 하자. 여기에서 새로운 random variable �=�2+� 를 정의하면, � 는 �=� 로 주어졌을 때, (�2,�2+110) 에 균등하게 분포된다. 이 분포의 joint pdf를 구하면 다음과 같다.
��,�(�,�)=5 , −1<�<1 and �2<�<�2+110
이 분포는 당연히 � 와 � 가 서로 독립이지 않다. 오히려 상당히 강한 연관 관계를 가진다.

이제 이 분포의 covariance를 구해보자.
Cov(�,�)=�[��]−�[�]�[�]=�[�(�2+�)]−�[�]�[�2+�]=�[�3+��]−�[�](�[�2+�])=�[�3]+�[�]�[�]−�[�]�[�2]−�[�]�[�]
이 때 �는 -1부터 1까지 균등하게 분포되어 있으므로 �[�]=�[�2]=�[�3]=0 이다. 따라서 Cov(�,�)=0 이다.
위 예제에서 � 와 � 는 상당히 강한 연관 관계인데도 불구하고 covariance와 correlation이 0이 된다. 왜 이렇게 되는 것일까? 그것은 covariance와 correlation은 여러 연관 관계 중 선형 관계만을 표현하는 지표이기 때문이다.
THEOREM
1. −1≤���≤1
2. |���|=1 ⇔ �(�=��+�)=1 을 만족하는 �≠0, � 가 존재한다.
3. ���=1 인 경우 2번에서 �>0, ���=−1 인 경우 �<0.
이 정리에 따르면, 만약 � 와 � 의 분포가 어떤 직선 �=��+� 에 몰려있다고 한다면, correlation은 -1 또는 1에 가까운 값이 될 것이다. 그러나 그러한 직선이 존재하지 않는다면, correlation은 0이 될 것이다. 위의 예제는 그러한 직선이 존재하지 않기 때문에 correlation이 0이 된 것으로 해석할 수 있다. Example 1의 경우 ��,� 와 ��,� 의 correlation을 비교해보면, ��,� 가 1에 더 가깝다. 분포 그래프에서도 ��,� 가 더 직선에 가깝게 분포해 있음을 알 수 있다.
(증명)
1. 다음과 같은 함수 ℎ(�) 를 정의해보자.
ℎ(�)=�[{(�−��)�+(�−��)}2]
이 함수를 � 로 전개하면,
ℎ(�)=�[(�−��)2]�2+2�[(�−��)(�−��)]�+�[(�−��)2]=��2�2+2Cov(�,�)�+��2
ℎ(�) 는 정의상 random variable의 제곱의 기대값이므로 �의 값과 상관없이 언제나 0보다 크거나 같아야 한다. 따라서 � 에 대한 2차 함수가 � 의 값과 상관없이 언제나 0보다 크거나 같을 조건
(Cov(�,�))2−��2��2≤0
정리하면,
−����≤Cov(�,�)≤����
따라서,
−1≤���≤1
2. |���|=1 이기 위해서는 위의 증명에서 판별식=0 이어야 한다. 즉, ℎ(�)=0 인 점이 중근을 가져야 한다. 그러나 ℎ(�) 는 정의상 random variable의 제곱의 기대값이므로 그 외의 모든 경우 0보다 크다. 따라서
�([(�−��)�+(�−��)]2=0)=1
이어야 한다. 따라서 중근에서는
�((�−��)�+(�−��)=0)=1
가 성립한다. 이를 다시 정리하면,
�(�=−��−���+��)=1
3. ℎ(�)=0 일 때, 2차 방정식의 근의 공식으로부터 �=−Cov(�,�)��2 를 얻는다. 따라서 3번 내용이 성립한다.
(증명 끝)
#Advanced Topics
1. Relationship between covariances and inner products
Covariance의 기본 성질들을 살펴보면, inner product1의 정의와 일치한다는 것을 알 수 있다. 실제로 연속인 random variable들의 집합을 mean zero를 equivalence relation으로하여 quotient set을 정의하고, second moment가 finite한(즉, variance가 존재하는) random variable만으로 부분 집합을 만들면 이 집합은 vector space가 된고 covariance는 이 vector space의 real-valued �2 inner product가 된다. 이러한 관점에서 식 (???)은 사실상 Cauchy-Schwarz inequality를 적용하는 것과 같다. 따라서 다음과 같이 Cauchy-Schwarz inequality를 증명하는 방식으로도 증명할 수 있다.
다음과 같은 random variable � 를 정의하자.
�=�−Cov(�,�)��2�
그러면 covariance의 성질에 의하여,
0≤��2=Cov(�,�)=Cov(�−Cov(�,�)��2�,�−Cov(�,�)��2�)=��2−(Cov(�,�))2��2
만약 random variable을 복소수 영역까지 확장시킨다면, inner product의 정의로부터 covariance의 성질 Cov(�,�)=Cov(�,�) 는 다음과 같이 수정되어야 한다.2
Cov(�,�)=Cov(�,�)―
이러한 성질을 만족하도록 covariance를 다음과 같이 재정의할 수 있다.
DEFINITION
Random variable � 와 � 에 대하여, 다음 값을 � 와 � 의 covariance라고 부른다.
Cov(�,�)=�[(�−��)(�−��)―]
- inner product의 자세한 내용은 (선형대수학) 4.1 Inner Product Space 참고 [본문으로]
- \(\overline{A}\)는 \(A\)의 complex conjugate이다. [본문으로]
'통계 > 기초통계' 카테고리의 다른 글
| [통계] [기초통계] 4. 정규분포 문제풀이 (0) | 2024.01.19 |
|---|---|
| [통계] [기초통계] 왜도 skewness 설명 (0) | 2024.01.19 |
| [통계] [기초통계] 6. 모평균 및 모비율의 신뢰구간 구하는 법 설명 (0) | 2024.01.19 |
| [통계] [기초통계] 베르누이분포 설명 (0) | 2024.01.19 |
| [통계] [기초통계] 3. 조건부 확률 설명 (1) | 2024.01.19 |


