[통계] [기초통계] Z test 설명
https://blog.naver.com/oooasd73/221610919338
#8. 심리통계 Z검정(Z test), T검정(T test)
안녕하세요. 두두의 심리블로그 '두두'입니다. 심리통계 8번째 시간에는 Z검정과 T검정을 다뤄...
blog.naver.com
1. Z검정(Z-test)
1. 단일표본 Z검정
Z검정에서 처음 다룰 것은 단일표본 Z검정입니다. 우선, Z검정은 Z분포를 가지고 모집단의 통계치와, 나(연구자)의 통계치를 비교하는 방법입니다. 이를 비교하기 위해선 표준정규분포를 이용하여 가설을 검증합니다. 지난 정규분포와 표준정규분포에서 Z값에 대해 다루었는데, 기억이 안 나신다면 그 포스팅을 참고해주세요.
단일표본 Z검정은 말 그대로 표본이 1개 있는 것으로 하나의 표본을 가지고 비교를 하는 방식입니다.
단일표본 Z검정의 기본 가정은,
① 종속변수가 양적변수 ② 정규분포 가정 ③ 등분산 가정 ④ 모집단의 분산을 알고 있을 때
입니다. 여기서 ④번이 중요한 것은 모집단의 분산을 알지 못하면 Z검정을 사용할 수 없습니다. 그때는 이후 다룰 T검정을 사용하게 돼요.
단일표본 Z검정의 검정 절차는 아래와 같습니다.
1. H0, H1를 세우고, a(알파), n(표본)을 설정
2. x bar(평균)을 계산
3. SE(표준오차) 계산
4. Z 통계치 계산
5. p-value와 a 비교 or z값으로 비교
6. 통계적 기각여부 확인
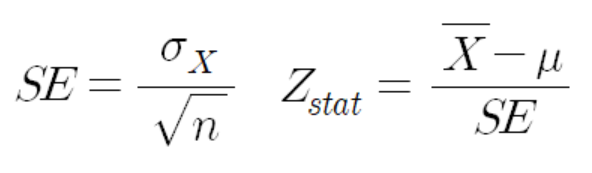
SE(표준오차) 와 Z stat
이를 문제에 대입해보겠습니다.
|
예제1)
지난 오랜 기간 동안 두두고등학교 학생들의 수학 점수를 알아보았는데, 평균 점수는 75점 표준편차는 15점인 정규분포를 따랐다. 올해 2019년도에 두두고등학교 100명의 학생들을 대상으로 수학점수를 확인하였더니 평균점수가 79.5점이 나왔다. 2019년도에 실시한 수학점수와 이전 수학점수 간의 평균이 같은지 유의수준 a=.05에서 검정하고자 한다.
|
여기서, Z검정의 ④ 번째 특징인 모집단의 분산을 알아야한다는 점을 충족하고 있으므로 Z검정을 사용합니다. 또한, 평균이 '같은지'를 검정하는 것이므로 양측검정을 사용합니다(등호 =, ≠ 사용). 유의수준은 0.05로 언급이 되었는데, 유의수준이 전혀 언급이 되지 않았을 경우에는 사회과학의 기본인 0.05를 사용하시면 됩시다. 앞서 말씀드린 공식 절차를 이용한다면,
1. 귀무가설 H0 : u=75, 대립가설 H1 : u ≠ 75
2. 유의수준(a:알파) = 0.05,
순서대로, SE(표준오차), Z stat에 대입을 하면 나(연구자)의 통계치가 3.0이 나오게 됩니다.
이제 모집단의 표준정규분포와 나의 Z값을 비교하면 되는데요, '같은지'를 검정하는 것이기 때문에 '양측검정'을 사용하여야 합니다.
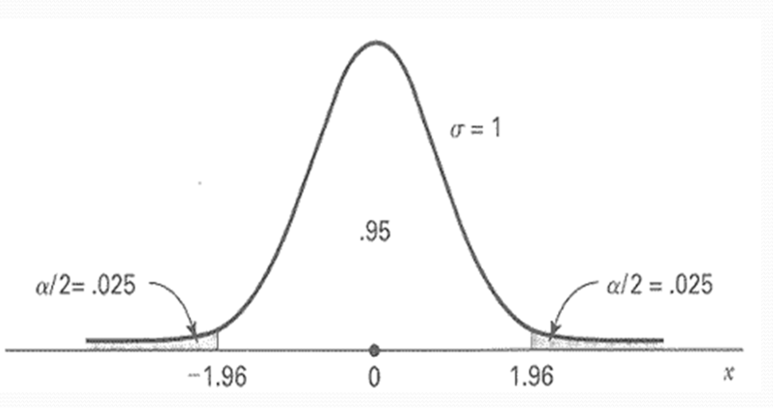
양측검정일 경우, 유의수준(a:알파)이 양쪽으로 나뉘어져 1/2로 나눠 계산
왼쪽 오른쪽 그래프 양쪽을 검정하는 것이기 때문에 유의수준도 2로 나눠 계산해야 합니다. 그렇게 되면 유의수준 a= .025가 되고, 0.025의 Z값은 1.96이 됩니다. 하지만 우리의 Z값은 3.0이기 때문에 그래프 상 더 극단값 쪽으로 향하게 됩니다. 그렇게 되면 귀무가설을 기각하게 되므로 대립가설을 받아들이게 됩니다.
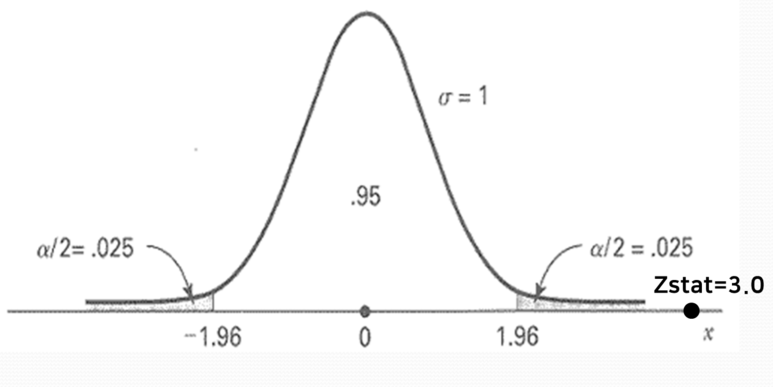
나(연구자)의 통계치는 유의수준 보다 더 작고, 극단값에 향해 있으므로 귀무가설을 기각한다
Z stat 값을 p-value로 변환하면, 0.00135가 됩니다.
p-value= .00135 < a/2= .0025
Z stat= 3.0 > Z crit= 1.96
이므로, 귀무가설을 기각합니다.
* 결론 : 두두고등학교의 수학점수 평균은 통계적으로 이전의 수학점수 평균과 다르다.
라는 결론이 내려지게 됩니다.
여기서 Z stat 값을 p-value로 변환하는 과정이 쉽지 않으므로(저 역시 R 프로그램으로 변환) Z값끼리 비교하면 편합니다. 여기서 주의해야할 점은, p-value는 값이 유의수준보다 작아야 귀무가설을 기각하는 것이고, Z값은 더 커야 귀무가설을 기각한다는 점입니다.
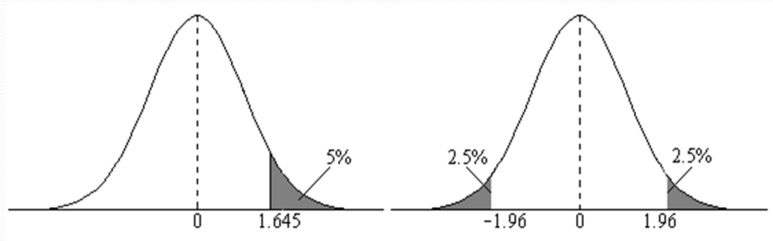
일방향 검정(좌측 그래프)과 양방향 검정(우측 그래프)
또한, 앞서 #7. 가설검정 파트에서 설명했듯이, 일방향 검정과 양방향 검정이 나뉘어지게 되는데요. 일방향 검정은 말 그대로 한 방향으로의 검정이기 때문에 그래프의 우측을 가지고 비교합니다. 반대로 양방향은 양쪽 좌우 모두를 검정해야 하기 때문에 유의수준을 절반으로 나눠서 계산합니다.
주로, 통계적으로 검정할 때 '같은지, 차이가 있는지'와 같은 문장이 들어가면 양방향 검정. '높은지, 낮은지'와 같은 문장이 들어가면 일방향 검정을 사용합니다.
2. 두 표본 Z 검정
방금은 단일표본 Z검정이었다면, 이번에는 표본이 2개인 두표본 Z검정입니다. 계산 절차는 단일표본 Z검정과 동일하지만 SE와 Z stat값을 구하는 식은 다르니 이 점을 유의해주시면 되겠습니다.
|
예제2)
연구자 '두두'가 전국 20대 남녀 100명을 무작위로 뽑아 몸무게를 측정하였는데, 남자의 평균 몸무게는 68kg, 여자는 50kg이었다. 또한, 20대 모집단 남자의 체중 표준편차는 10kg이고 여자는 9kg을 알고 있다. 여기서 20대 남녀의 체중이 차이가 있는지 여부를 검정하여라.
|
여기서 모집단의 표준편차를 알고 있으므로 Z검정, 유의수준이 언급되지 않을 때는 0.05로 설정하므로 a=.05로 설정합니다. 또한 남자와 여자라는 두 표본이 있으므로 두 표본 Z검정을 사용합니다.
1. 귀무가설 H0 : u1=u2(차이 없다), 대립가설 H1 : u1 ≠ u2(차이 있다)
2. 유의수준(a:알파) = 0.05,
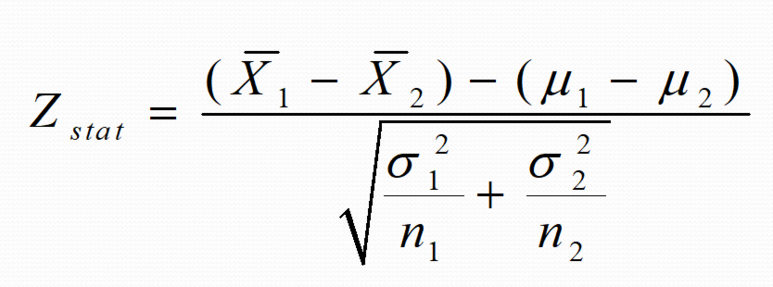
두 표본 Z검정의 Z stat 식
두 표본 Z검정의 식은 위와 같습니다. 차례 대로 대입을 하게 되면,
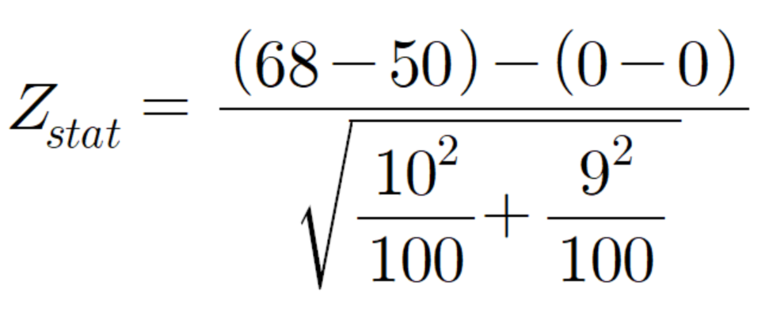
Zstat 식 대입.
위와 같은 식이 나오게 됩니다. 최종적으로 계산을 하면,
Zstat = 13.3792946324이 나오게 됩니다. 이때, 양방향 검정이므로 a=.025에서 검정을 하게 되면,
Zstat 13.38 > Zcrit 1.96 이므로, 귀무가설을 기각하게 되고 결론적으로 20대 남녀의 몸무게 차이는 있는 것으로 통계적으로 증명 가능하게 됩니다.
※ 여기서 Z stat 식에서 (u1-u2) 이게 왜 (0-0)이 됐는지 궁금하신 분들이 많을 겁니다. 그 이유로는, 우리는 가정할 때 귀무가설이 참임을 먼저 가정을 하고 시작한다고 하였습니다. 저희가 계산 절차에서 첫 번째로 귀무가설, 대립가설을 세웠는데요.
< 1. 귀무가설 H0 : u1=u2(차이 없다), 대립가설 H1 : u1 ≠ u2(차이 있다) >
바로 여기서 귀무가설 u1=u2라고 가정했기 때문에 u1-u2는 0이 되는 것입니다.
3. 단일 표본 비율 검정, 두 독립 표본 비율 검정
단일 표본 비율 검정과 두 독립 표본 비율 검정도 사실 다를 게 없이 '비율'로 들어갔다는 점, 표본이 하나인지 두개인지에 따라 달라진다는 점입니다. 앞서 말씀드린 바와 비슷하므로 공식 위주로 언급하겠습니다.
- 단일 표본 비율 검정
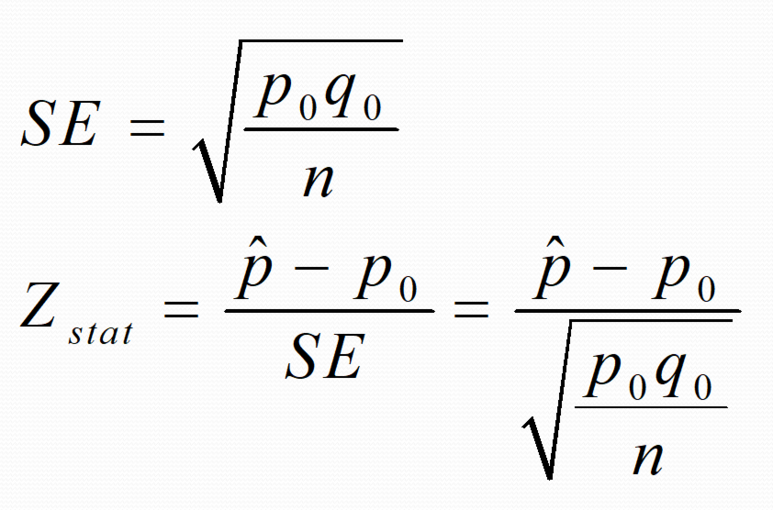
단일표본 비율검정 SE, Zstat
여기서 p0는 문제에서 언급되는 모집단의 비율이며, q0은 1-p0입니다. p hat은 우리가 알고 있는 비율입니다. 즉, 문제에서 '모집단의 반대 비율이 0.6이었고, 이를 토대로 이번에 연구를 했을 때, 반대비율은 0.5였다'라고 했을 때, p0=0.6, q0=(1-p0)이므로 1-0.6 = 0.4가 됩니다. 또한, p hat은 우리가 조사를 통해 알게 된 비율이므로 0.5가 됩니다.
- 두 독립표본 비율 검정
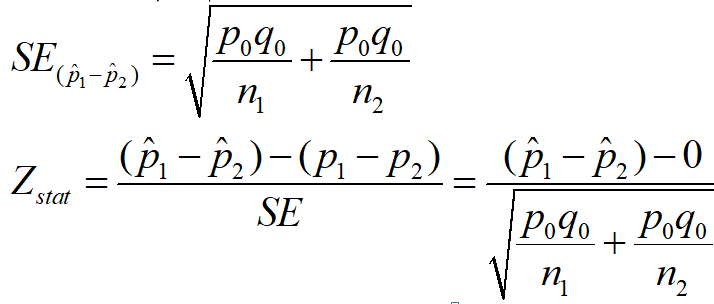
두 독립 표본 비율 검정의 SE, Zstat
위의 식과 같습니다. 표본이 두 개이기 때문에 더 복잡할 수밖에 없는데요. 문제에 주어진 식을 잘 파악하고 대입하기만 한다면 문제 없이 풀 수 있습니다. 그러나,모집단의 비율을 알 수 없는 문제가 주어지는 경우가 많습니다.
|
예제3)
연구자 '두두'가 서울시 '자전거 따릉이'에 착안을 받고 경기도에도 이 제도를 도입하려고 30대 여성 200명, 남성 250명을 추출하여 찬성 여부를 물은 결과, 여성은 140명 찬성으로 찬성비율 .7, 남성은 75명 찬성으로 찬성비율 .3이었다. 유의수준 .05로 정하였을 때, 두 비율 간의 차이가 있는지 통계적으로 검정하시오
|
라고 주어졌다고 가정합시다. 이때, 문제를 보시면 모집단의 비율이 언급되지 않습니다. 그러면 저희는 SE를 구할 수가 없게 되죠. 그럴 경우에 통합비율을 사용하게 됩니다.
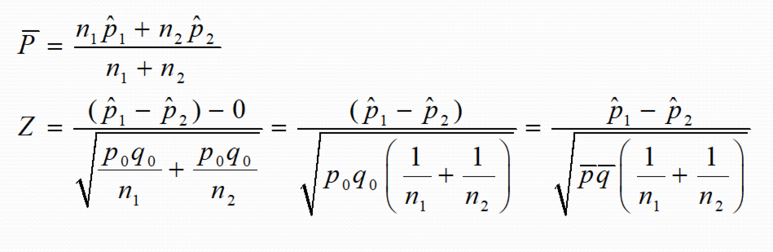
통합비율(맨 위 식) p bar, Z stat
통합비율 p bar식을 나열하며 위 식과 같습니다.
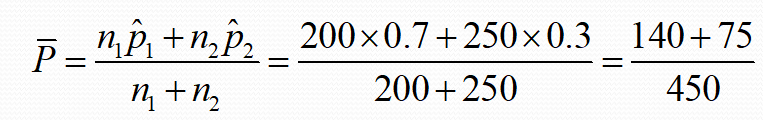
통합비율에 대입한 식
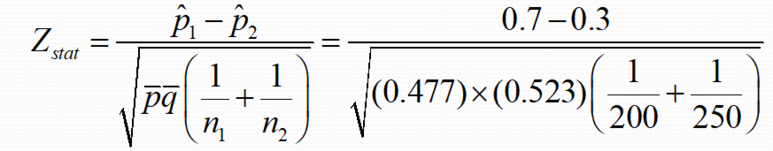
Zstat에 대입한 식
결과적으로 식을 차례대로 대입해서 풀면, Z=8.44가 나오게 됩니다. 그렇게 되면 Zcrit이 1.96이기 때문에 Zstat값이 더욱 크므로 귀무가설을 기각하고 두 비율 간 차이가 있다는 것을 결론내게 되죠.
2. T검정(T-test)
1. 단일표본 T검정
다음은 T검정입니다. T검정은 표본의 크기가 작을 때 (주로 20개 이하) 사용하며, 두 집단 간의 평균 차이를 검정하는 방법입니다. 이 단일표본의 가정은 이렇습니다.
① 종속변수가 양적변수 ② 종속변수 값이 정규분포라고 가정 ③ 등분산 가정(두 집단 T검정만) ④ 모집단의 분산을 모를 때
입니다. 먼저 T분포는 표본의 크기가 작기 때문에 표본의 크기가 증가하면 증가할수록 정규분포를 따르게 되고 Z검정에 가까워진다는 가정이 있습니다.
단일표본 T검정의 검정 절차는 아래와 같습니다.
1. H0, H1를 세우고, a(알파), n(표본)을 설정
2. x bar(평균), Sx(표준편차) 계산
3. SE(표준오차) 계산
4. t 통계치 계산
5. p-value와 a 비교 or t값으로 비교
6. 통계적 기각여부 확인
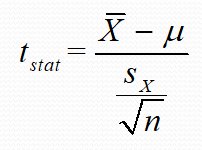
t stat의 값
보시면 검정 절차는 Z절차와 거의 동일합니다. 그대신 문제에서 '모집단의 분산(표준편차)'가 주어지지 않는 다는 점입니다. 하지만 표본의 표준편차는 식으로 주어지기 때문에 이를 대입하시면 됩니다.
2. 두 표본 T 검정
두 표본 T검정은 말 그대로 표본이 2개인 경우인데요, 이 역시 두 표본의 n수, 표준편차, 평균이 주어지기 때문에 식에 대입만 하시면 됩니다.
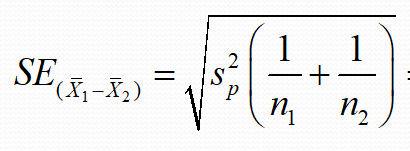
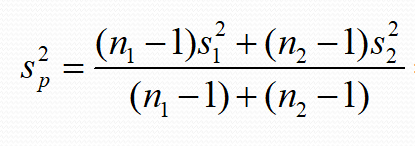
좌측 표준오차, 우측 통합분산
두 표본의 통합분산을 구해야 표준오차를 구할 수 있는데요, 통합분산의 식을 우측에 있는 식과 같습니다.
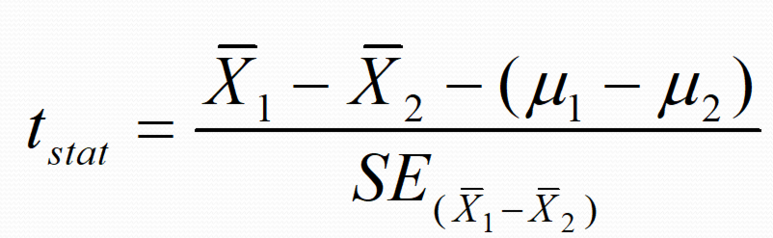
최종적으로 tstat에 대입하여 풀면 통계적으로 accept하는지 reject하는지 알아낼 수 있습니다. 두 표본 t검정에서 자유도는 (n1-1)+(n2-1)로 전체사례수-2입니다. 자유도에 따라 tcrit이 바뀌게 되므로 주의하셔야 합니다. 특히 Z검정과 T검정의 또 다른 차이는 z table t table이 다르다는 것인데요, Z값에서 1.96은 a=.025였습니다. 하지만 t table에서의 a=.025는 t stat= 2.262로 다르므로 표를 보실 때 자유도와 함께 고려하여 확인하여야 합니다.
3. 종속 표본 t 검정
마지막으로 종속 표본 t검정인데요. 집단 간 서로 종속이 되어 있어서 종속표본 t검정이라고 합니다.
위 식처럼, 사후검사는 사전검사에 종속이 되어 있기 때문에 이러한 전, 후 효과비교에 대한 검정은 종속표본 t검정을 사용하시면 됩니다. 우선 (사전검사-사후검사)를 통해 d값을 알아내시고,d값의 평균을 구합니다 (평균 = 1.6)
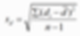
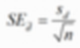
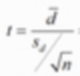
그리고 차례대로 식을 대입하면 t=4로 나오게 됩니다. 종속표본 t검정에서의 자유도는 (n-1)입니다!
t-test는 주로 사회과학 분야에서 많이 쓰이는 통계입니다. 그 이유로는, 우선 모집단의 분산을 알 수 없는 경우가 대다수이기 때문에 t-test를 많이 이용하고 있죠.
이로써 긴 Z검정 T검정 정리를 마쳤습니다...!!
'통계 > 기초통계' 카테고리의 다른 글
| [통계] [기초통계] [포아송 분포] (1) | 2024.01.19 |
|---|---|
| [통계] [기초통계] 1. 표본과 표본평균 (1) | 2024.01.19 |
| [통계] [기초통계] 왜도 skewness 설명 (0) | 2024.01.19 |
| [통계] [기초통계] 5. 신뢰구간 설명 (1) | 2024.01.19 |
| [통계] [기초통계] 4. 정규분포 문제풀이 (0) | 2024.01.19 |



