모집단으로부터 무작위로 n개의 표본을 추출했을 때, 이 n개 표본들의 평균과 분산을 각각 '표본평균(sample mean)', '표본분산(sample variance)'라고 합니다.
무작위 표본(random sample)은 다음과 같은 가정을 가집니다.

그럼 표본평균부터 알아보죠.

표본평균은 직관적으로 알 수 있습니다. 이제 표본분산을 알아보려고 합니다. 분산은 편차의 제곱의 기댓값이죠.
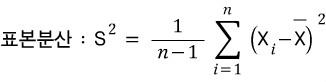
이제 표본평균을 새로운 확률변수라고 생각해 봅시다. 그럼 여기서 표본평균의 평균과 분산을 또 구할 수 있겠죠.
※ 표본평균을 구했는데 어떻게 표본평균을 새로운 확률변수라 생각하고 평균과 분산을 구하냐는 댓글이 있어 추가로 설명합니다. 한 가지 예를 들어보죠. 대한민국 남성의 평균 신장을 구하려고 합니다. 하지만 모든 남성의 키를 전부 측정하는 것은 불가능하므로 몇 명만 선발해서 키를 측정해야 합니다. 지역별로 남성을 뽑아 측정한다고 해보죠. 서울, 부산, 대구, 대전, 광주, 인천 등등... 지역별로 얻은 남성 신장의 평균과 분산은 어느정도 비슷하겠지만 전부 다릅니다. 따라서 이 지역별 평균 신장을 이용해 또 평균과 분산을 구할 수 있죠. 즉, 지역별 평균 신장을 새로운 확률변수로 생각하는 것 입니다. 따라서 표본평균이 보여주는 분포도 존재하는 것이죠. 이것을 sampling distribution of the mean 이라고 합니다. 나중에 회귀분석에서 오차를 이해하는데 중요한 개념으로 이용됩니다.

여기서 하나 의문이 가는게 n개의 표본을 추출했는데, 표본평균은 n으로 나누고 왜 표본분산은 (n-1)로 나누는 걸까요?? 아래를 보시죠.

표본은 모집단의 부분집합이므로, 표본평균 및 표본분산은 모집단의 성격을 잘 보여줘야 합니다. 따라서 표본분산의 기댓값은 모집단의 분산(모분산)이 되어야 합니다.

위에서 유도한 과정이 바로 표본분산은 n이 아닌 (n-1)로 나눠줘야 하는 이유입니다. 만약 (n-1)이 아니라 n으로 나눠줬다면 표본분산의 기댓값은 모분산이 나오지 않았겠죠. (n-1)로 나눠주는 이유를 좀 더 자세히 알고 싶으면 아래 링크주소를 참고하시기 바랍니다.(키워드 : Bessel's correction)
Bessel's correction : https://en.wikipedia.org/wiki/Bessel%27s_correction
Bessel's correction - Wikipedia
From Wikipedia, the free encyclopedia Correction for sample variance bias In statistics, Bessel's correction is the use of n − 1 instead of n in the formula for the sample variance and sample standard deviation,[1] where n is the number of observations
en.wikipedia.org
'통계 > 기초통계' 카테고리의 다른 글
| [통계] [기초통계] 상관계수 구하기 (0) | 2024.01.20 |
|---|---|
| [통계] [기초통계] [포아송 분포] (1) | 2024.01.19 |
| [통계] [기초통계] Z test 설명 (0) | 2024.01.19 |
| [통계] [기초통계] 왜도 skewness 설명 (0) | 2024.01.19 |
| [통계] [기초통계] 5. 신뢰구간 설명 (1) | 2024.01.19 |



